Numpy Dot, Explained

In this tutorial, I’ll show you how to use the Numpy dot function (np.dot), to compute dot products in Numpy.

I’ll explain exactly what the function does, how the syntax works, and I’ll show you clear examples of how to use np.dot.

Table of Contents:

• Introduction
• Syntax
• Examples
• FAQ

If you need something specific, you can click on any of the above links, and it will take you to the appropriate section of the tutorial.

Having said that, if you’re new to Numpy, or need a quick refresher about mathematical dot products, you should probably read the whole tutorial.

A Quick Introduction to Numpy Dot

First of all, let’s start with the basics.

What does Numpy dot do?

At a high level, Numpy dot computes the dot product of two Numpy arrays.

If you’re a little new to Numpy though, or if you don’t completely understand dot products, that might not entirely make sense.

So let’s quickly review some basics about Numpy and about dot products.

Numpy dot operates on Numpy arrays

Let’s start with Numpy.

As you’re probably aware, Numpy is an add-on package for the Python programming language.

We mostly use Numpy for data manipulation and scientific computing, but we use Numpy on specific types of data in specific data structures.

Numpy is a Package for Working with Numeric Data in Python

In particular, Numpy creates and operates on Numpy arrays.

A Numpy array is a data structure that stores numerical data in a row and column structure.

So for example, a 2-dimensional Numpy array looks something like this:

Numpy arrays can come in a variety of shapes and sizes. For example, we can build 1-dimensional arrays, 2-dimensional arrays, and n-dimensional arrays.

Additionally, we can create Numpy arrays where the Numbers have a variety of different properties. For example, we can create arrays that contain normally distributed numbers, numbers drawn from a uniform distribution, numbers that are all the same value, just to name a few.

So Numpy has a variety of functions for creating Numpy arrays with different types of properties.

Numpy has Functions for Performing Calculations with Numpy Arrays

In addition to having functions for creating Numpy arrays, the Numpy package also has functions for operating on and computing with Numpy arrays.

So Numpy has many functions for performing mathematical computations, like computing the sum of an array, computing exponentials of array values, and many more.

Additionally, Numpy has functions for doing more advanced operations, like operations from linear algebra.

np.dot computes dot products in Numpy

So what does the Numpy dot function do?

The simple explanation is that np.dot computes dot products.

To paraphrase the entry on Wikipedia, the dot product is an operation that takes two equal-length sequences of numbers and returns a single number.

Having said that, the Numpy dot function works a little differently depending on the exact inputs.

There are three broad cases that we’ll consider with np.dot:

• both inputs are 1D arrays
• both are 2D arrays
• one inputs is a scalar and one input is an array

Let’s take a look at how Numpy dot operates for these different cases.

If the input arrays are both 1-dimensional arrays, np.dot computes the vector dot product

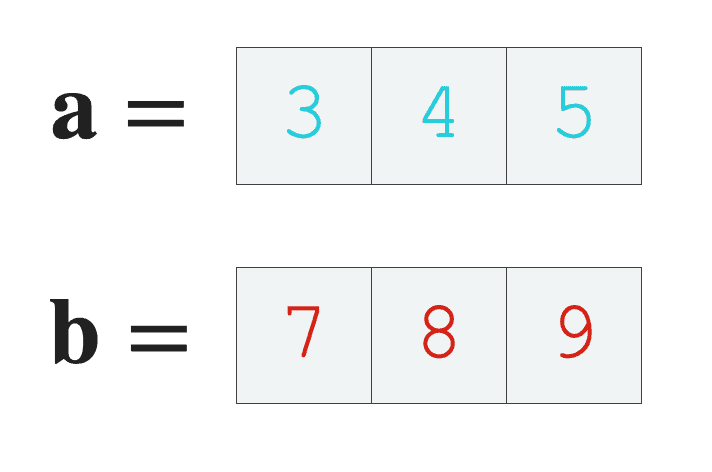
Let’s say we have two Numpy arrays, and , and each array has 3 values.

Given two 1-dimensional arrays, np.dot will compute the dot product.

The dot product can be computed as follows:

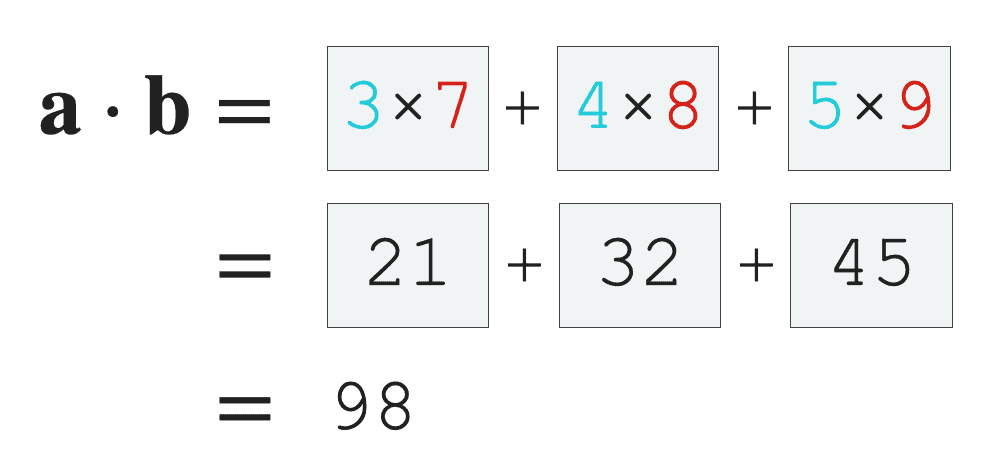
Notice what’s going on here. These arrays have the same length, and each array has 3 values.

When we compute the dot product, we multiply the first value of by the first value of . We multiply the second value of by the second value of . And we multiply the third value of by the third value of . Then, we take the resulting values, and sum them up.

The output is a single scalar value … in this example, .

In mathematical terms, we can generalize the example above. If we have two vectors and , and each vector has elements, then the dot product is given by the equation:

(1)  

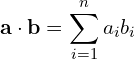
Essentially, when we take the dot product of two Numpy arrays, we’re computing the sum of the pairwise products of the two arrays.

If one of the inputs is a scalar, np.dot performs scalar multiplication

The second case is when one input is a scalar value , and one input is a Numpy array, which here we’ll call .

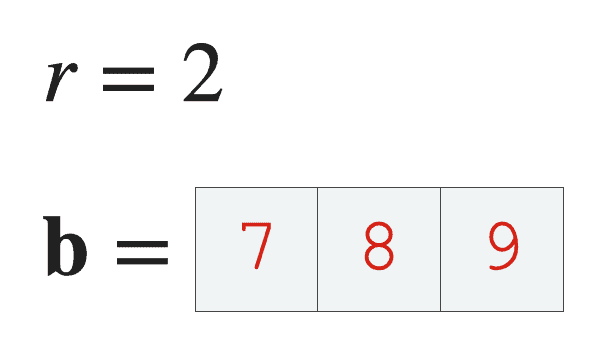
If we use Numpy dot on these inputs with the code np.dot(r,b) Numpy will perform scalar multiplication on the array:

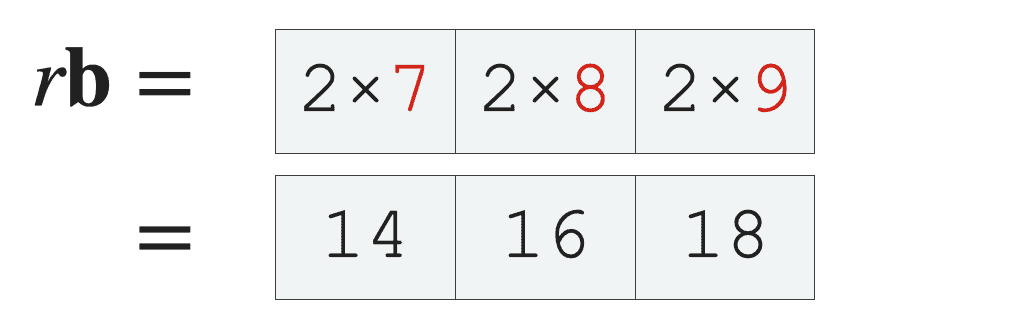
So when we use Numpy dot with one scalar and one Numpy array, it multiples every value of the array by the scalar and outputs a new Numpy array.

If both inputs are 2D arrays, np.dot performs matrix multiplication

The final case that we’ll cover is when both of the input arrays are 2-dimensional arrays.

In this case, with two 2D arrays, the np.dot function will perform matrix multiplication.

A full explanation of matrix multiplication is beyond the scope of this tutorial, but let’s look at a quick example.

Let’s say that you have two 2D arrays, and .

Next, let’s multiply those arrays together using matrix multiplication.

During matrix multiplication, we multiply the values of the rows of with the values of the columns of and sum them up in the following way:

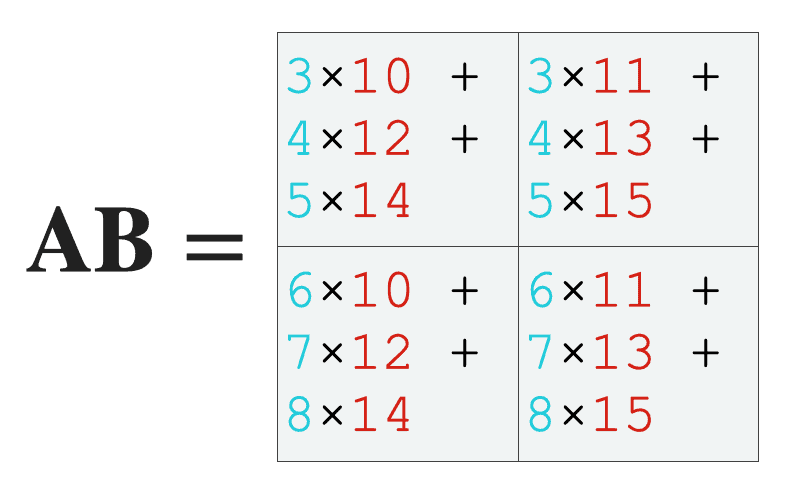
And here’s the final computed output:

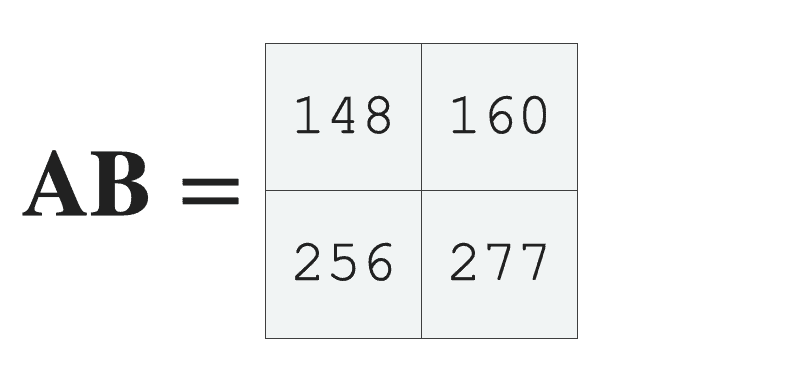
Notice that the output array, , has the same number of rows as and the same number of columns as .

Additionally, each value in the output array is calculated by summing the product of the ith row of and the jth row of .

More generally, to compute the output array , each value of the output array is defined as:

(2)  

If you’re not familiar with linear algebra generally, and matrix algebra specifically, I realize that these equations can be a little confusing. Maybe even a little intimidating.

That said, if you want to learn more about these operations, I recommend that you read the book Linear Algebra and its Applications, by David Lay and colleagues. It’s a very approachable book about linear algebra that will help you understand some of the operations we’re performing with Numpy dot.

Ok. So now that we’ve looked at what Numpy dot does, let’s take a closer look at the syntax.

The Syntax of Numpy Dot

Here, I’ll explain the syntax of the Numpy dot function.

A quick note

One thing before we look at the syntax.

In order to use Numpy functions, you need to import Numpy first. You can do that with the following code:

import numpy as np

This is important, because how you import Numpy will affect the syntax.

It’s the common convention among Python data scientists to import Numpy with the alias ‘np‘, and we’ll be sticking with that convention here.

np.dot syntax

The syntax of np.dot is really very simple.

Assuming that you’ve imported Numpy with the alias np, you call the function as np.dot().

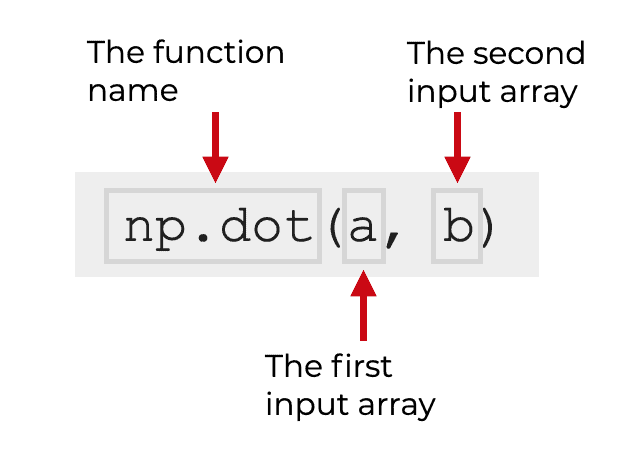
Then, inside the parenthesis, there are a few parameters that allow you to provide inputs to the function.

Let’s take a look at those inputs.

The parameters of np.dot

There are 2 core parameters for the np.dot() function.

• a
• b

Let’s quickly take a look at those, one by one.

a (required)

The a parameter allows you to specify the first input value or array to the function.

Technically, the argument to this parameter can be a scalar value, or any “array-like” object.

Because it allows array-like objects, this can be a proper Numpy array, or it can be a Python list, a tuple, etc. A scalar value like an int or float will also work.

Keep in mind that you must provide an argument to this parameter.

b (required)

The b parameter allows you to specify the second input value or array to the function.

Similar to the a parameter, the argument to b can be a scalar value, or any “array-like” object. So acceptable arguments to this parameter include Numpy arrays, Python lists, and tuples. Scalar values like an int or float are acceptable as well.

Keep in mind that you must provide an argument to this parameter.

out (optional)

Note that np.dot() also has an out parameter. This is somewhat rarely used, so we’re not going to cover it here. For more information about this parameter, review the official documentation.

The output of np.dot

The output of np.dot() depends on the inputs.

There are a few cases:

• If both inputs are scalars, np.dot() will multiply the scalars together and output a scalar.
• If one input is a scalar and one is an array, np.dot() will multiply every value of the array by the scalar (i.e., scalar multiplication).
• If both inputs are 1-dimensional arrays, np.dot() will compute the dot product of the inputs
• If both inputs are 2-dimensional arrays, then np.dot() will perform matrix multiplication.

So as you can see, the output really depends on how you use the function.

With that in mind, let’s take a look at some examples so you can see how it works, and see the different types of outputs that np.dot() produces given certain types of inputs.

Examples: How to Compute Dot Products in Numpy

Ok. Let’s work through some step-by-step examples.

If you need something specific, you can click on any of the following links, and it will take you to the approprate example.

Examples:

• Multiply two numbers
• Multiply a Number and an Array
• Compute the Dot Product of Two 1D Arrays
• Perform Matrix Multiplication on Two 2D Arrays

Run this code first

Before you run any of the examples, you’ll need to import Numpy first.

You can do that with the following code:

import numpy as np

Once you’ve done that, you should be ready to go.

EXAMPLE 1: Multiply two numbers

Ok. Let’s start with a simple example.

Here, we’re going to use two numbers (i.e., scalar values) as the inputs to np.dot().

np.dot(2,3)

OUT:

6

Explanation

This is maybe a little unexpected, but very simple.

Here, we called np.dot() with two scalar values, 2 and 3.

When we call np.dot() with two scalars, it simply multiplies them together.

Obviously 2 * 3 = 6.

EXAMPLE 2: Multiply a Number and an Array

Next, let’s provide an array and scalar as inputs.

Here, we’ll actually provide a scalar (an integer) and a Python list. Instead of a Python list, we could also provide a Numpy array, but I’ve used a Python list instead because it makes the operation a little easier to understand here.

Let’s take a look.

np.dot(2,[5,6])

OUT:

array([10, 12])

Explanation

Again, this is very simple.

The first argument to the function is the scalar value 2.

The second argument to the function is the Python list [5,6].

When we provide a scalar as one input and a list (or Numpy array) as the other input, np.dot() simply multiplies the values of the array by the scalar.

Mathematically, we’d consider this to be scalar multiplication of a vector or matrix.

EXAMPLE 3: Compute the Dot Product of Two 1D Arrays

Next, let’s input two 1-dimensional lists.

Here, we’ll use two Python lists, but we could also use 1D Numpy arrays. I’m using Python lists because it makes the operation a little easier to understand at a glance.

Let’s take a look.

np.dot([3,4,5],[7,8,9])

OUT:

98

Explanation

What’s going on here?

Here, the np.dot() is computing the dot product of the two inputs.

These inputs are 1-dimensional Python lists. And as I said earlier, we could also use 1D Numpy arrays.

Mathematically, 1D lists and 1D Numpy arrays are like vectors.

When we’re working with vectors and take the dot product, the dot product is computed by equation 1 that we saw earlier.

   

So when Numpy dot has two 1D lists or arrays as inputs …

… it takes the product of the pairwise elements, and then adds them together:

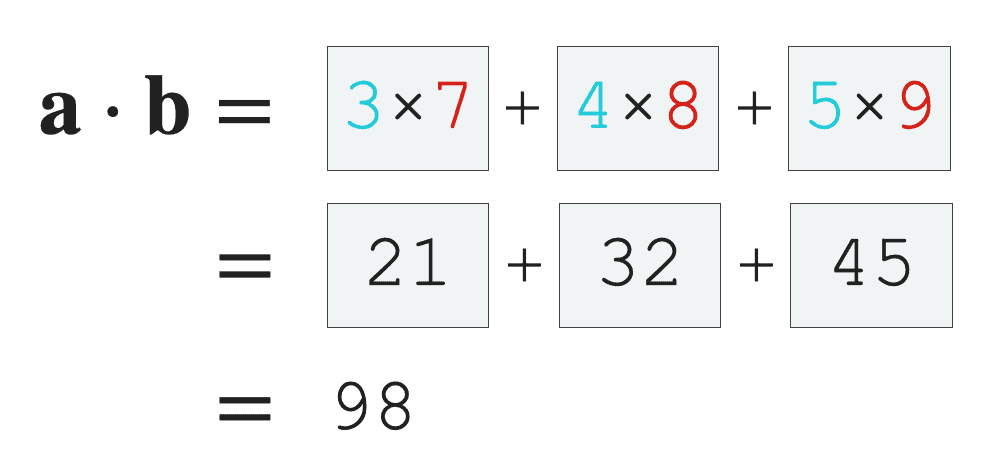
And the output is a scalar value. In this case, the result is 98.

EXAMPLE 4: Perform Matrix Multiplication on Two 2D Arrays

Finally, let’s look at what happens when we use Numpy dot on two 2-dimensional arrays.

Create Arrays

First, let’s just create two 2-dimenstional Numpy arrays.

To do this, we’ll use the np.arange() function to create a sequence of numbers, and then use the Numpy reshape method to reshape the numbers into a 2D shape.

A_array_2d = np.arange(start = 3, stop = 9).reshape((2,3))
B_array_2d = np.arange(start = 10, stop = 16).reshape((3,2))

And let’s print them out, just so you can see the contents.

print(A_array_2d)

OUT:

[[3 4 5]
 [6 7 8]]

print(B_array_2d)

OUT:

[[10 11]
 [12 13]
 [14 15]]

Notice that both of these Numpy arrays are 2-dimensional. Having said that, the number of rows in A_array_2d is the same as the number of columns in B_array_2d.

Use np.dot

Ok. Now let’s use the Numpy dot function on these two arrays.

np.dot(A_array_2d, B_array_2d)

OUT:

array([[148, 160],
       [256, 277]])

Explanation

So what happened here?

In this case, we used two 2-dimensional Numpy arrays as the inputs.

When we use 2D arrays as inputs, np.dot() computes the matrix product of the arrays.

When it does this, it np.dot() calculates the values of the output array according to equation 2 that we saw earlier.

   

So under the hood, this is what Numpy is doing when we run the code np.dot(A_array_2d, B_array_2d) :

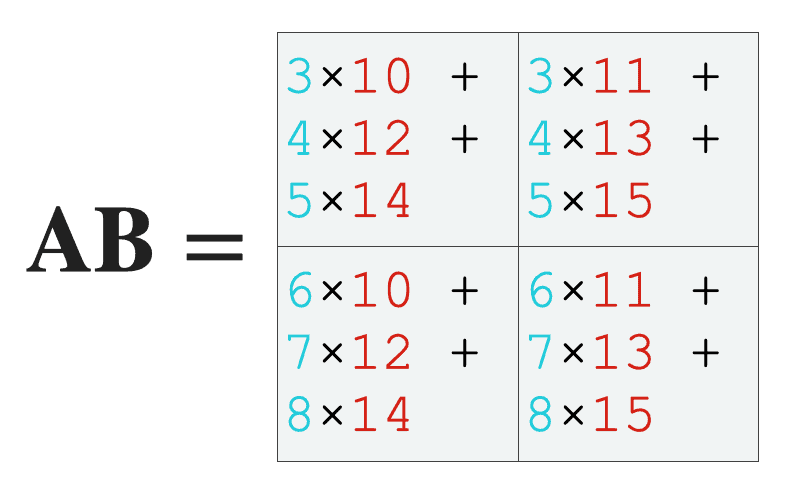
Look carefully. In the above image, you can see that the computation multiplies the values of the rows of A by the values of the columns of B, sums them up, and puts them into the final output array, with the following values:

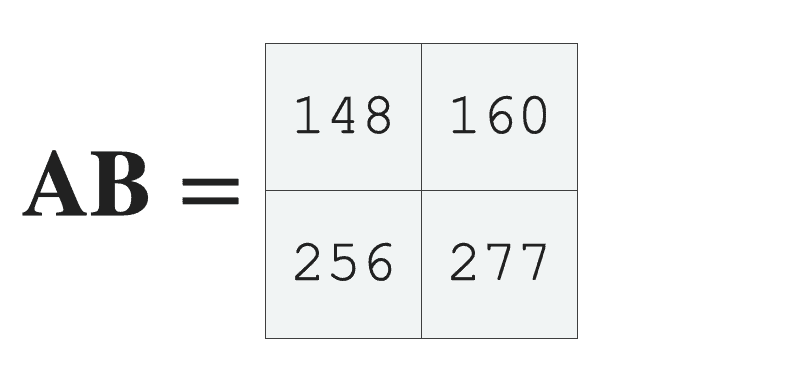
This operation is known as the matrix product.

So again: when we use Numpy dot on two 2-dimensional arrays, np.dot() computes the matrix product.

I understand that this might be slightly confusing if you don’t have a lot of experience with linear algebra. If that’s the case, I recommend that you do some reading about linear algebra generally, and matrix multiplication in particular.

Frequently asked questions about Numpy Dot

Now that we’ve looked at some examples, let’s look at a few common questions about the np.dot() function.

Frequently asked questions:

• What’s the difference between np.dot() and np.matmul() ?
• What’s the difference between np.dot() and ndarray.dot() ?

Question 1: What’s the difference between np.dot() and np.matmul() ?

Numpy dot and Numpy matmul are similar, but they behave differently for some types of inputs.

The two big differences are for:

• multiplication by scalars
• multiplication of high-dimensional Numpy arrays

Let’s look at these one at a time.

Multiplication by scalars

The first difference between np.dot() and np.matmul() is that np.dot() allows you to multiply by scalar values, but np.matmul() does not.

As we saw in example 2, when we use np.dot() with one scalar (e.g., an integer) and an array/list, Numpy dot will simply multiply every value of the array by the scalar value.

np.dot(2,[5,6])

OUT:

array([10, 12])

However, if you try to do this with np.matmul() you’ll get an error:

np.matmul(2,[5,6])

OUT:

ValueError: matmul: Input operand 0 does not have enough dimensions (has 0, gufunc core with signature (n?,k),(k,m?)->(n?,m?) requires 1)

Multiplication of high-dimensional arrays

The second area where np.dot() and np.matmul() are different is when they operate on high-dimensional arrays.

According to the doccumentation …

When you use np.dot:

If a is an N-D array and b is a 1-D array, it is a sum product over the last axis of a and b.

If a is an N-D array and b is an M-D array (where M>=2), it is a sum product over the last axis of a and the second-to-last axis of b:

But when you use np.matmul:

If either argument is N-D, N > 2, it is treated as a stack of matrices residing in the last two indexes and broadcast accordingly.

Ultimately, np.dot() and np.matmul() behave differently for scalar multiplication, and for multiplication of higher-dimensional inputs.

Question 2: What’s the difference between np.dot() and ndarray.dot() ?

np.dot() and ndarray.dot() are very similar, and effectively perform the same operations.

The difference is that np.dot() is a Python function and ndarray.dot() is a Numpy array method.

So they effectively do the same thing, but you call them in a slightly different way.

Let’s say we have two 2-dimensional arrays.

A_array_2d = np.arange(start = 3, stop = 9).reshape((2,3))
B_array_2d = np.arange(start = 10, stop = 16).reshape((3,2))

We can call the np.dot() function as follows:

np.dot(A_array_2d, B_array_2d)

But we use so-called “dot syntax” to call the .dot() method:

A_array_2d.dot(B_array_2d)

The output is the same, but the syntax is slightly different.

If you’re still confused about this, make sure to read more about the difference between Python functions and Python methods.

Leave your other questions in the comments below

Do you still have questions about the Numpy dot function?

If so, leave your questions in the comments section below.

Join our course to learn more about Numpy

In this tutorial, I’ve explained how to use the np.dot() function to compute dot products of 1D arrays and perform matrix multiplication of 2D arrays.

This should help you understand np.dot, but if you really want to learn Numpy, there’s a lot more to learn.

If you’re serious about mastering Numpy, and serious about data science in Python, you should consider joining our premium course called Numpy Mastery.

Numpy Mastery will teach you everything you need to know about Numpy, including:

• How to create Numpy arrays
• What the “Numpy random seed” function does
• How to reshape, split, and combine your Numpy arrays
• How to use the Numpy random functions
• How to perform mathematical operations on Numpy arrays
• and more …

Moreover, this course will show you a practice system that will help you master the syntax within a few weeks. We’ll show you a practice system that will enable you to memorize all of the Numpy syntax you learn. If you have trouble remembering Numpy syntax, this is the course you’ve been looking for.

Find out more here:

Learn More About Numpy Mastery