In machine learning, making sure that you have a model that performs well is, in some sense, the most important thing.
This means that you need to be really good at evaluating different models.
But, this can be a challenge, as you run into issues like overfitting, hyperparameter optimization, and model selection.
One way to overcome these various model evaluation and selection challenges is with cross validation.
Cross validation is a set of related techniques that we can use to evaluate and optimize our machine learning models.
And, it’s a very important tool in the toolkit of a machine learning developer.
So in this post, I’m going to explain the essentials of cross validation.
I’ll explain what it is, give a crystal clear example to help you understand, and I’ll explain some of the challenges associated with cross validation.
If you need something specific, you can click on any of these following links:
Table of Contents:
- Cross Validation Basics
- Why Cross Validation is Important in Machine Learning
- The Main Types of Cross Validation
- Special Concerns and Considerations with Cross Validation
- Best Practices and Tips for Effective Use of Cross Validation
Let’s jump in.
Cross Validation Basics
Cross validation is a very important technique for evaluating the performance of machine learning systems.
At its core, cross validation is about assessing how well a machine learning model generalizes to new, previously unseen data.
This is critical, because in many cases, a model may perform very well on the training data, but fail to perform well on new data that was outside of the training dataset. This situation, called overfitting, is when a model performs well on the training dataset, but then fails to perform on validation or test sets (or worse, performs well on the training data, but fails to perform well in production).
Avoiding overfitting is one of the core problems of machine learning. To say that mitigating overfitting is one of the top 5 problems of building machine learning might actually be undestating the problem. It’s that important.
And because it’s so important, you really need to understand how to minimize, correct, or otherwise mitigate overfitting.
Although there are several ways to fix overfitting – like using a validation set, regularization, and others – one of the most important is cross validation.
WTF is Cross Validation
There are several different types of cross validation (sometimes called CV for short), but let’s start out with a simple explanation of what cross validation is.
The basic concept behind cross validation is taking the training data and splitting it into segments. We use one segment as the validation data (to evaluate the performance of the model), and the rest of the segments to train the model.
So, it’s sort of like a split of the data into training and validation data.
BUT, it’s more complicated than a simple training/validation split.
To illustrate, let’s look at k-fold cross validation.
K-Fold Cross Validation
K-fold cross validation is a fairly simple process.
In k-fold cross validation, we:
- Split the data into k folds.
- Train the model on k-1 of the folds (i.e., train the model on all of the folds, except one).
- Evaluate the model on the kth holdout fold by computing performance on a metric.
- Rotate the folds, and repeat steps 2 and 3, with a new holdout fold. Repeat steps 2 and 3 until all of the k folds have been used as the holdout fold exactly 1 time.
- Average the model performance across all iterations
Ok, ok. That might sound a little complicated.
But it’s actually easy to understand with a visual example.
So let’s look at an example of 5-fold cross validation in action.
Example of 5-Fold Cross Validation
I think that it’s easiest to understand 5-fold cross validation (and k-fold cross validation generally) with a picture.
At a high level, this is what we’re doing in 5-fold cross validation:
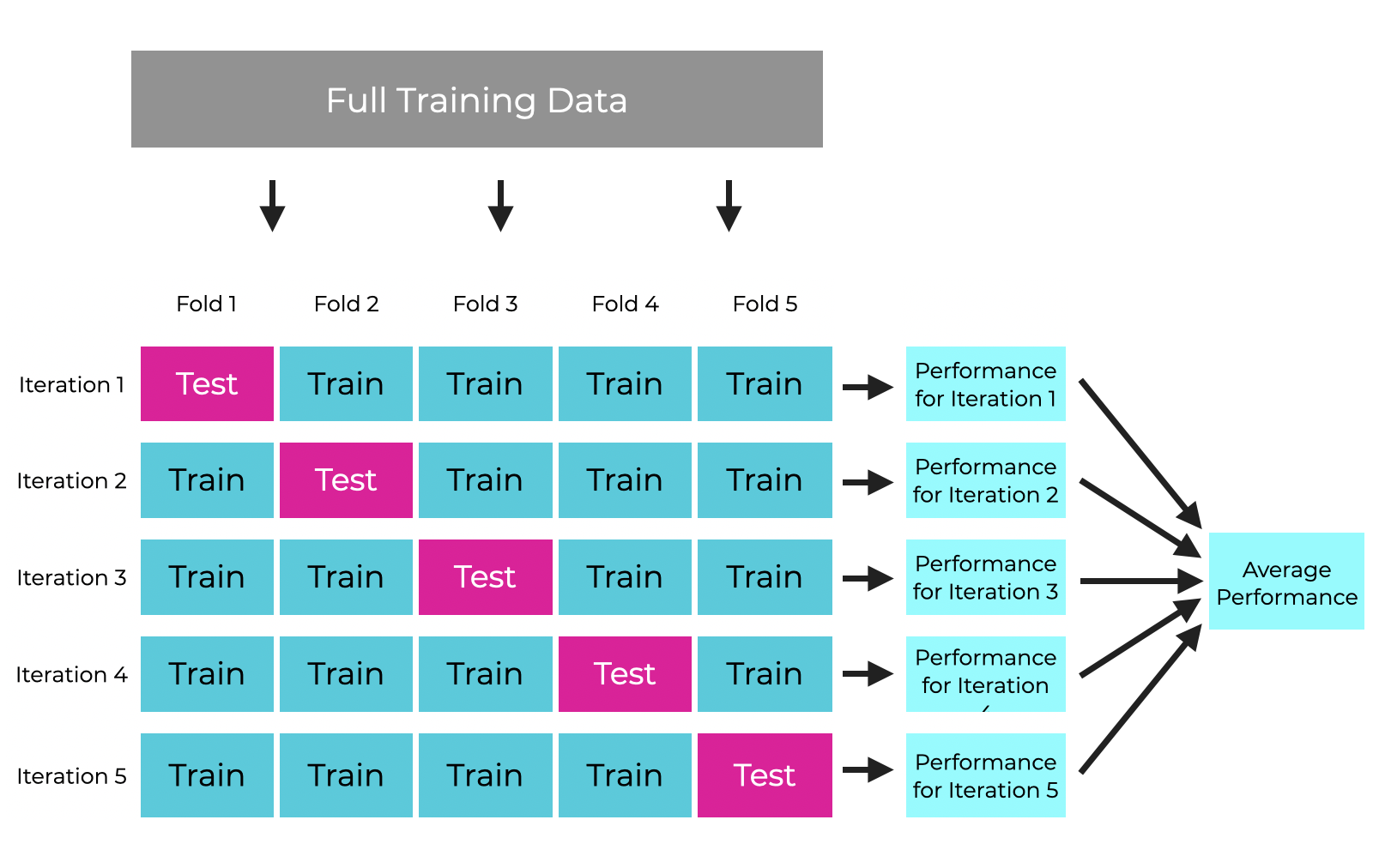
Notice what’s happening.
We take the training data and we split it into folds. In the case of 5-fold cross validation we split the data into 5 folds (as you might expect).
Then we train and validate the model multiple times, during multiple iterations.
During every iteration, we select 1 of the folds as the validation set. Then we train the model on the remaining 4 folds. During every iteration, we select a new fold as the validation set and then train and validate the model again.
For every iteration, we compute the performance of the newly trained model.
After we iterate through all of the folds (such that every fold has been used exactly 1 time as the validation set), then we average the results across all folds.
Although there are some complexities with k-fold CV, as well as some advantages and disadvantages that you need to consider when using it, I think that it’s somewhat easy to understand if you have a good visual image to help explain it.
All that said, let’s discuss why cross validation is so important in machine learning development.
Why Cross Validation is Important for Machine Learning
Cross validation is critical in machine learning because it’s essential for model evaluation. But because it’s so good at evaluating models, it’s also one of the primary tools that we use to compare different models, and this in turn helps us tune model hyperparameters.
Cross Validation is a Critical Model Evaluation Tool
Cross validation is an indispensable tool for model evaluation in machine learning.
And the major reason for this is that cross validation provides a more comprehensive and robust assessment of a model’s performance, compared to a simple train/validation split.
This advantage comes from how cross validation performs multiple rounds of training and validation.
Recall from my explanation above that in cross validation, we split the data into segments (e.g., folds, in k-fold cross validation) and then iteratively train the model on k-1 of the segments, validate the model on the kth segments, and then repeat that process multiple times, using every segments as the validation set exactly one time.
Effectively, cross validation is like performing a train/validation split multiple times and then averaging the results.
This evens out the peculiarities that might exist in a single test set.
And in turn, it provides us with a more reliable and robust evaluation of the performance of the model.
Cross Validation Helps us Compare Models
Because cross validation provides us with a more robust way to evaluate the performance of individual models, it’s also a more robust way to compare models.
When we use a single train/validation split, we run the risk that a particular split of the data may favor one model over another. This could be due to certain idiosyncrasies in the training data for that particular split, such that the training data fails to represent the overall data.
In such a scenario, one model or algorithm might perform better on that one, idiosyncratic split.
In turn, this might make it appear that the “better performing” model is better generally but in reality, it’s just due to the particular random split that we made.
Cross validation mitigates this issue somewhat by splitting the data into segments (e.g., folds) and rotating those folds into the training and validation sets.
This helps ensure that we evaluate every model across a broader range of possible datasets, which ensures that the evaluation of each model better reflects the model’s ability to generalize.
Cross Validation is Essential For Hyperparameter Tuning
Further, cross validation plays a critical role in hyperparameter tuning.
Recall that hyperparameters are the parameters that the data scientist or machine learning engineer manually sets prior to the model training process. Hyperparameters contrast with run-of-the-mill “parameters” which are learned during model training. So “parameters” are learned via exposure to data, but “hyperparameters” are manually set by the developer.
The challenge with hyperparameters is selecting the optimal values. This becomes even more complicated when you have multiple hyperparameters.
For example, in a vanilla, feedforward neural network, there are many different hyperparameters, like:
- number of layers
- number of neurons per layer
- batch size
- learning rate
- the number of training epochs
- the choice of activation function
And more.
For most of those hyperparameters, there are multiple different settings or values. For example, there are at least a half dozen activation functions you could use (actually, more than that). For the number of layers, you could have as few as 1 layer and as many as hundreds of layers. The same for the number of neurons.
Because every one of those hyperparameters has multiple values, and there are multiple values for each hyperparameter, there’s potentially tens of thousands … even millions of different combinations of hyperparameter settings.
How do you choose the best combination of hyperparameter settings?
Again, it comes back to being really good at model evaluation.
And in some sense, it’s just a variation of model comparison and selection. But instead of choosing between different algorithms, when you’re evaluating different hyperparameter settings, you’re often trying to choose between models that use the same algorithm, but just different hyperparameter settings.
In order to do this properly, you need to be able to identify the hyperparameter settings that perform well across a range of different training datasets. You need to identify the combination of hyperparameter settings that will generalize to previously unseen data.
Cross Validation helps Mitigate Overfitting
Perhaps one of the biggest reasons that cross validation is important for machine learning development is that it helps mitigate overfitting.
Cross-validation helps prevent overfitting by ensuring that the performance of a model generalizes.
Said differently, cross validation makes sure that model performance isn’t overly tailored to a single, particular training dataset.
In traditional model training, a model might perform exceptionally on the training data but perform poorly on new, previously unseen data … a phenomenon known as overfitting.
Cross-validation combats this by dividing the data into multiple sets, and then training and validating the model repeatedly multiple times.
By repeating the training and validation process several times, with different data partitions each time, cross-validation helps ensure that the model generalizes well rather than just memorizing specific training data patterns.
The Main Types of Cross Validation
Having explained what cross validation is, and why it’s useful, let’s briefly discuss the main types of cross validation.
There are several types of cross validation, but the main ones that you should know are:
- k-fold cross validation
- stratified cross validation
- leave-one-out cross validation
- grouped cross validation
All of these forms of cross validation are similar in that they work over multiple iterations. We split the data, then train and validate multiple times.
What’s different about the the different types of cross validation is how they split the data.
Let’s quickly discuss each of these.
K-Fold Cross-Validation
I explained k-fold cross validation previously in this article, but let me briefly touch on it again.
K-fold cross validation is the most popular form of cross validation.
In k-fold cross validation, we divide the training data into ‘k’ equally-sized subsets, which are known as folds.
Then, during every iteration, one of the folds is held out as the validation set on which we evaluate the model.
And we train the model on the remaining k-1 folds.
We repeat this process k times, with each of the k folds used exactly once as the validation set.
Then we average the results from all k iterations to produce a single estimate of model performance.
Stratified K-Fold Cross-Validation
Stratified k-fold cross validation is more common in classification tasks (i.e., where the target variable is a categorical label).
In stratified k-fold cross validation, the process ensures that when we split the data into folds, every fold of the dataset has the same proportion of observations with a particular class.
This method of cross validation is particularly useful when we’re dealing with imbalanced datasets.
Leave-One-Out Cross-Validation (LOOCV)
Leave-one-out cross validation, which is also known as LOOCV, is a special case of k-fold cross validation, where ‘k’ is the number of examples in the dataset.
So if the dataset that you’re using has 100 examples, LOOCV will have 100 folds, and it will operate over 100 iterations.
Therefore, when we use leave-one-out cross validation, during every iteration, we use only one example as the test point on which we validate the model. And all of the remaining examples are used to train the model.
Leave-one-out cross validation can produce robust evaluations of your models, but it’s also very computationally expensive. It’s particularly computationally expensive for large datasets. Therefore, you may want to limit the use of LOOCV to situations where you have a small dataset, or when you have a very large amount of computational resources.
Grouped Cross-Validation
We use grouped cross validation when the data has groups or clusters of related points (i.e., where points within a group are related, and points in separate groups are unrelated or less related).
In such a situation, points within a particular group should be kept together instead of potentially being assigned to different folds (as could happen in k-fold cross validation).
So in grouped cross validation, examples in a particular group are always kept together in either the training set or the test set, but never split into both.
Monte Carlo Cross Validation (Repeated Training/Test Splits)
One more type of cross validation is Monte Carlo cross validation (AKA, repeated training/test splits)
Monte Carlo cross validation is a little different than k-fold.
Instead of splitting the data into k different folds, and then rotating the folds into the validation set (with the remaining data in the training set), Monte Carlo repeatedly splits the data randomly into training and test sets.
So whereas in k-fold cross validation, the algorithm splits the data into k-folds, and those folds are kept the same over every iteration, in Monte Carlo cross validation, there’s a new split of the data at every iteration. The algorithm just randomly splits the data into training and test, multiple times.
This can create some different behavior from k-fold cross validation.
In k-fold cross validation, every example will be in the “test” set exactly one time. But in Monte Carlo cross validation, it’s possible that an example can appear in the test set one time, multiple times, or zero times. It just depends on how the algorithm randomly splits the data in the iterations.
Different Cross Validation Schemes have Different Strengths and Weaknesses
I should note here that different cross validation schemes have different strengths and weaknesses.
Because this is a very big subject, it’s difficult to cover everything here in a single blog post.
That said, I’m going to write more about these different CV schemes individually in separate blog posts, and I’ll also write more comparisons of the different schemes, so you know when to use which type of cross validation.
Special Concerns and Considerations with Cross Validation
Although cross validation is a powerful tool for model evaluation in machine learning, it also comes with some disadvantages and limitations that wee need to consider to ensure that we use it most effectively.
Let’s talk about them.
Cross Validation has High Computational Costs
One of the biggest issues and limitations of cross validation, particularly methods like leave-one-out and Monte Carlo, is high computational cost.
Every fold or iteration in cross validation requires a separate training and validation step. In many instances, training a model a single time can be very time consuming, like when you train a deep neural network or boosted tree model.
Repeating training and validation multiple times then can become very time-consuming and computationally expensive.
This becomes even more of an issue when you’re working with large datasets or complex models.
To mitigate the issues with computational cost, you can:
- Use parallel computing to run cross-validation folds simultaneously, if resources permit.
- Use a smaller number of folds or iterations. Note that this might reduce the reliability of the model evaluation.
- Employ simpler models or dimensionality reduction techniques to reduce training time.
Of course, all of these have their own costs and/or tradeoffs.
Cross Validation Requires Specific Types of Data
Cross validation assumes that the data examples are independent and identically distributed (i.i.d.).
However, in many real-world tasks, data has a form that breaks this requirement.
For example, data can have groups, time dependences, or forms of correlation that make it hard or impossible to use certain types of cross validation.
To address this, you can:
- Use stratified or grouped cross-validation methods to handle datasets with imbalanced classes or group structures.
- Use time-series specific cross-validation techniques for time-series data or data with temporal dynamics.
Best Practices and Tips for Effective Use of Cross Validation
Before we close, let’s quickly cover some best practices for using cross validation in your machine learning development tasks.
- Always shuffle data before applying cross-validation, unless dealing with time-series data, to ensure random distribution of data across folds.
- Be mindful of the trade-off between the number of folds and the reliability versus computational cost. More folds generally provide a more reliable estimate but increase computational expense.
- In the case of hyperparameter tuning, use nested cross-validation to avoid overfitting. The outer loop helps in evaluating the model, while the inner loop selects the best hyperparameters.
- Regularly check for model performance consistency across different folds. Large variances might indicate an unstable model or issues with the data.
- When dealing with very small datasets, consider using leave-one-out cross-validation, as it maximizes the training data used.
Wrapping Up
Cross validation is a powerful tool for evaluating the ability of a model to generalize.
That said, cross validation should be used thoughtfully, since it also has increased computational costs and can introduce potential biases in the model.
Ultimately, you need to know the strengths and weaknesses of different cross validation techniques, which will enable you to select the right cross validation technique for your specific machine learning problem.
That said, I’m going to write more in the future about specific types of cross validation, as well as how and when to use it, how to optimize cross validation, how to deal with specific cross validation issues, etc.
Leave your Questions Below
Do you still have questions about cross validation?
Is there something else that you want me to explain?
I want to hear from you.
Leave your questions, concerns and comments in the comments section at the bottom of the page.
Sign up for our email list
If you want to learn more about data science and machine learning, then sign up for our email list.
Every week, we publish free long-form articles about a variety of topics in machine learning, AI, and data science, including:
- Machine Learning
- Scikit Learn
- Deep Learning
- Keras
- Numpy
- Pandas
- … and more
When you sign up for our email list, then we’ll deliver those tutorials to you, free, and direct to your inbox.