Perceptrons, Explained

by

Unless you’ve been living in cave somewhere in remote Eurasia, you should know that deep learning is very popular, and very powerful.

A variety of tools from self driving cars to Chat GPT use deep learning; they complex neural networks with many hidden layers.

In the modern Tech environment, it can be very valuable to understand deep learning and neural networks.

But before you understand deep learning – which is sort of an advanced topic – it helps to understand the simple foundations of neural networks.

In particular, it’s helpful to first learn about the simplest neural network structure, the artificial neuron, which we call a perceptron.

So being the generous guy that I am, I’m going to explain perceptrons in this blog post. I’ll explain what perceptrons are, how they’re structured, and how they fit into the bigger picture of deep learning and neural networks.

If you need something specific, just click on one of the following links.

Table of Contents:

A Quick Introduction to Perceptrons

You’re probably familiar with deep learning and artificial neural networks or at least heard the terms.

Perceptrons are related to deep learning and ANNs.

In fact, perceptrons are one of the simplest types of artificial neuron, so we can think of them as the foundation of neural networks.

Perceptrons are Based on Biological Neurons

Originally proposed in 1957, perceptrons were one of the earliest components of artificial neural networks.

The structure of the perceptron is based on the anatomy of neurons.

Neurons have several parts, but for our purposes, the most important parts are the dendrites, which receive inputs from other neurons, and the axon, which produces outputs.

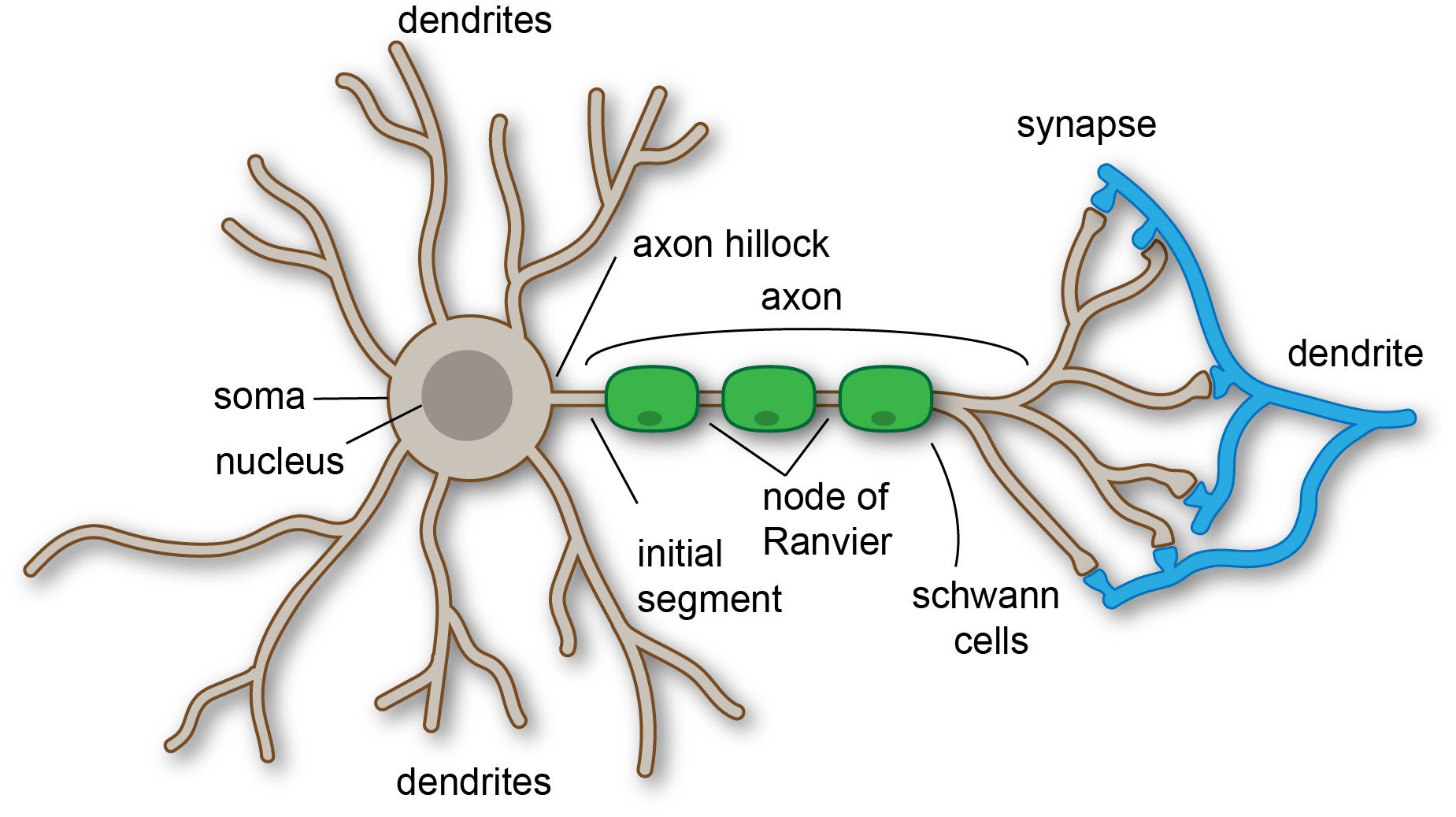
An image of the anatomy of a neuron.

The outputs of an axon can then serve as the inputs to the dendrites of another neuron (which allow neurons to operate in networks, like in the human brain).

Importantly, a neuron will produce an output only if it receives a sufficient number of input signals at the dendrites. Remember: neurons in a brain are organized into a network of many neurons. So the dendrites of a neuron typically receive inputs from many other neurons.

Neuron Activation

Neurons “fire” – that is, produce an output – in an all or nothing way. The outputs of a neuron are essentially 0 or 1. On or off.

A neuron will “fire” if the input signals at the dendrites are sufficiently large, collectively. If the amount of input signal at the dendrites is high enough, the neuron will “fire” an produce an output. But if the amount of input signal is insufficient, the neuron will not produce a output. Put simply, the neuron sums up the inputs, and if the collective input signals meet a certain threshold, then it will produce an output. If the collective input signals are under the threshold, it will not produce an output.

This is, of course, a very simple explanation of how a neuron works (because they are very complex at the chemical level), but it’s roughly accurate.

Why is this important?

Because scientists suggested that we would be able to create artificial neurons, modeled after animal neurons, which would be able to process input data in a similar way.

How Perceptrons are Structured

Perceptrons are essentially artificial neurons.

They have a very similar structure to biological neurons.

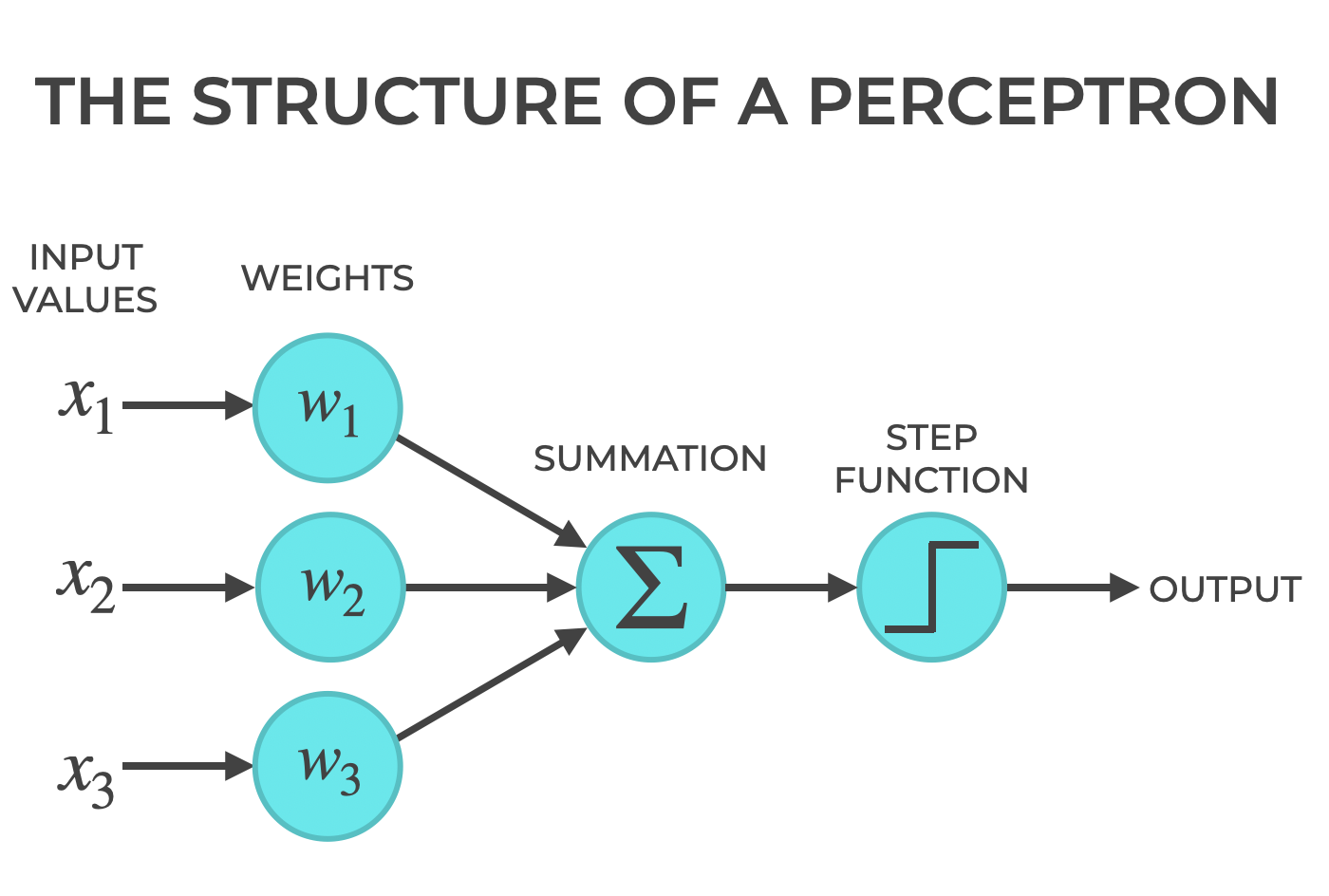
An image that visually explains the structure of a perceptron.

There are inputs, the inputs are weighted, and if the weighted inputs collectively reach a certain threshold, then the perceptron produces an output.

Let’s quickly discuss a few of these parts of a perceptron.

Inputs

Perceptrons have multiple numeric input values, x_i.

In a perceptron, these input x values can be real numbers.

However, in other artificial neuron models, the allowed input values are constrained. For example, in the McCulloch-Pitts neuron (which is slightly different from a perceptron), the input values are binary 0/1 values.

Weights

In a perceptron, every input value is multiplied by a weight, w_i.

So collectively, we have the inputs x_i, each multiplied by their respective weight, which produces the values x_iw_i.

Alternatively, if you think of the input x values as a vector \textbf{x}, and the weights also as a vector \textbf{w}, then the inputs multiplied by the vector can be thought of as the product \textbf{x}^\top\textbf{w}.

Summation

The perceptron takes the product of the inputs and the weights, and sums them up.

This can be represented with the equation:

(1)   \begin{equation*} \sum_{i = 1}^{n}x_iw_i \end{equation*}

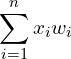
But in a perceptron and other forms of artificial neurons, we typically apply a function to these summed weighted inputs, which brings us to the activation function.

Step Function (i.e., Activation Function)

As you learn more about artificial neurons and neural networks, you’ll learn a lot more about activation functions.

An activation function is a function that’s applied to the summed inputs times weights, \sum_{i = 1}^{n}x_iw_i, to determine if the neuron should activate, and the exact form of the output if it does activate.

There are actually a variety of different activation functions, but the simplest is arguably the step function.

The step function, as the name implies, visually looks like a step.

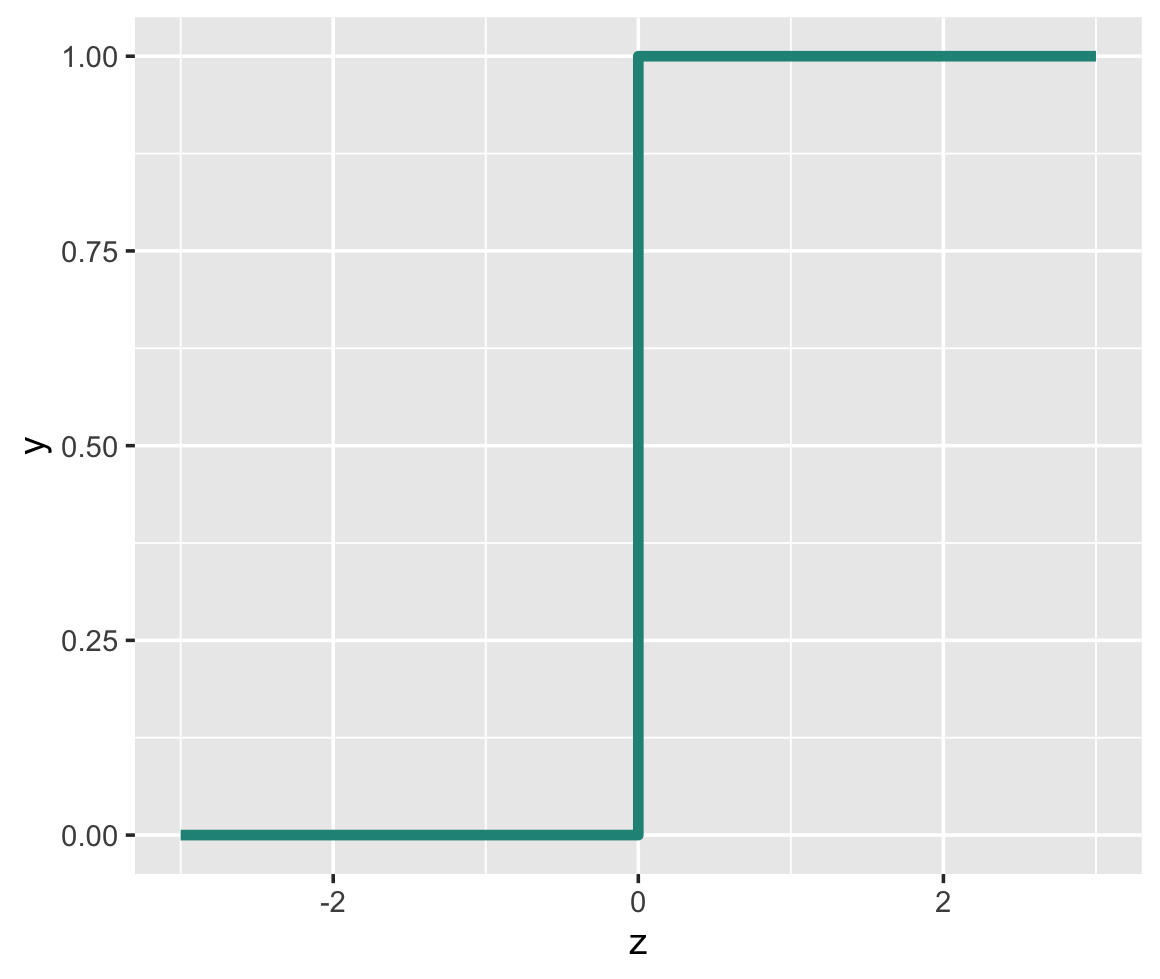
In the step function visualized above, if the input value is greater than 0, then the output of the step function is 1.

If the input value is less than 0 or equal to 0, then the output of the step function is 0.

So the step function forces the output into a binary 0/1 range.

The step activation function is important for the final output, which we’ll see in the next section.

Output

We can model the output of a perceptron like this:

(2)   \begin{equation*} \text{Output = Step(Weighted Sum of Inputs)} \end{equation*}

That’s sort of an English-language version.

A slightly more mathematical version is as follows:

(3)   \begin{equation*} \text{Output} = Step(\sum_{i = 1}^{n}x_iw_i)} \end{equation*}

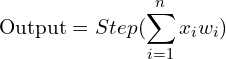
Again though, this assumes that we’re strictly using a step function as our activation function (i.e., that we’re modeling a traditional perceptron).

Perceptrons in Machine Learning and Deep Learning

So now that we’ve looked at the structure of a Perceptron, let’s talk about how we use them and where they sit in the overall discussion of machine learning and deep learning.

Perceptrons are a type of Binary Linear Classifier

Perceptrons are a type of simple machine learning model.

Most specifically, perceptrons are a type of classifier.

Recall what we discussed earlier about the step function output of Perceptrons. Perceptrons output either a 0 or 1, depending on whether the inputs collectively reach a threshold.

So, we can characterize a perceptron as a simple type of binary linear classifier.

By themselves, they can solve classification problems with 2 possible target classes, where the data are linearly separable.

We Can Combine Perceptrons into Networks

Although it’s possible to use a perceptron all by itself as a machine learning technique, they’re much more interesting when we combine them together.

One simple neural network architecture that uses perceptrons is the multilayer perceptron.

Put simply, a multilayer perceptron combines together multiple perceptrons into an architecture that has multiple “layers.”

A multilayer perceptron has an input layer and an output layer (much like a lone perceptron).

But importantly, multilayer perceptrons also have what’s called a “hidden layer.”

What’s a hidden layer?

A hidden layer is a layer of neurons between the input layer and the output layer.

So a multilayer perceptron architecture must have at least one hidden layer.

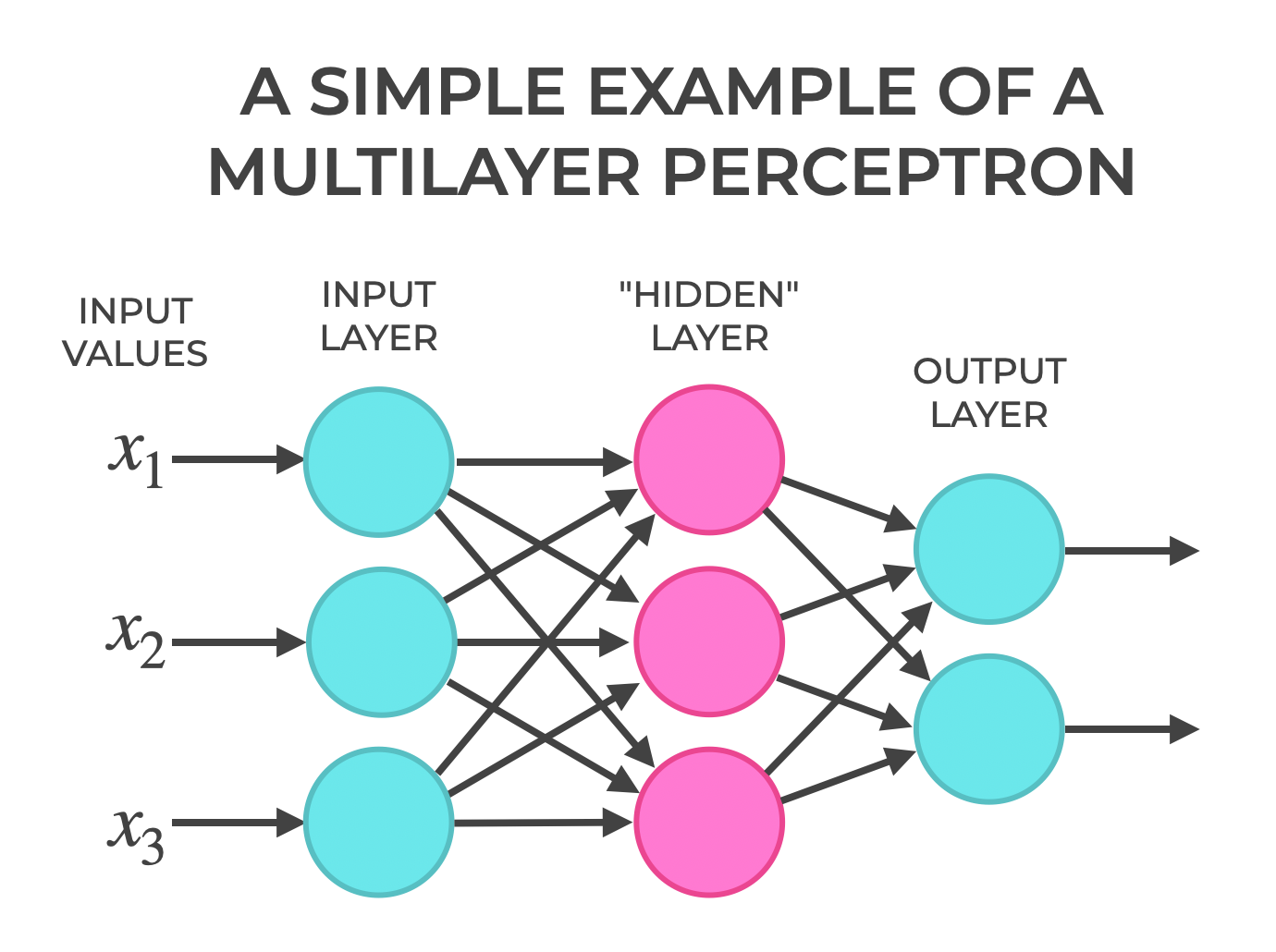
An image of a multi layer perceptron.

The addition of these hidden layers allows multilayer perceptrons to solve more complex problems.

Perceptrons and Multilayer Perceptrons Form the Foundation of Deep Learning

So why does all this matter?

Perceptrons are the foundation of multilayer perceptrons, and multilayer perceptrons form the foundation of deep learning.

One of the simplest deep network architectures is a multilayer perceptron with many stacks of hidden layers. A “deep” stack of hidden layers (that’s why we call it “deep” learning).

There’s More to Learn

I’ve tried to give you an overview of perceptrons in this blog post.

But, I’ve left a lot out.

Particularly when we start talking about multi layer perceptrons and deep learning, there are a lot of additional, relevant details.

So if you want to understand and use neural networks, there’s a lot more to learn.

For more tutorials about machine learning and deep learning, sign up for our email list

All that said, if you want to learn more about machine learning and deep learning, then sign up for our email list.

Here at Sharp Sight, we publish multiple tutorials per month about:

  • NumPy
  • Pandas
  • Base Python
  • Scikit learn
  • Machine learning
  • Deep learning
  • … and more.

And when you sign up for our email list, you’ll get these tutorials delivered direct to your inbox.

Joshua Ebner

Joshua Ebner is the founder, CEO, and Chief Data Scientist of Sharp Sight.   Prior to founding the company, Josh worked as a Data Scientist at Apple.   He has a degree in Physics from Cornell University.   For more daily data science advice, follow Josh on LinkedIn.

3 thoughts on “Perceptrons, Explained”

  2. I don’t understand the hidden layer diagramm. Does each percetron produce three outputs for each hidden layer percetron? The percetrons in the input layer should use all input data, not only one. Is it right?

    Reply

    • Every input should receive one input number (neural networks almost always use numeric data).

      Every output also produces a number.

      Neural networks can produce one output or multiple outputs depending on the task(s) and the architecture.

      I’ll write more about this in the future.

      Reply

Leave a Comment